Triton Fused Backward Layer Norm
This post will go over some of the overlooked details of fused backward layer norm implementation in triton. Here I will mostly go into the maths and visualization, for the complete code you can check the original Triton tutorial - Layer Normalization
First thing to cover is the derivation of Vector Jacobian Product of x, given by the formula below:
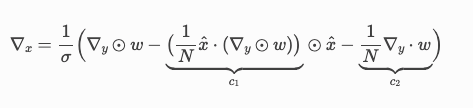
Here are some basic differentials that we will ultimately plug into the final formula.

Plugging all the above differentials into the main formula below we get our VJP of x.

We can also see the straightforward derivation of the VJPs of w and b above.
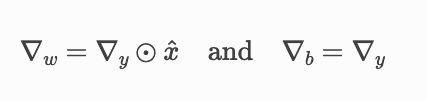
Now, since these each input in a batch will affect the gradient calculation of W and B, we will need to sum up the calculated dw and db matrix along the batch dimension. For summing the inputs along the batch we parallelize the sum in small groups, this partial sum (parallelized) is finally reduced again to get the output.
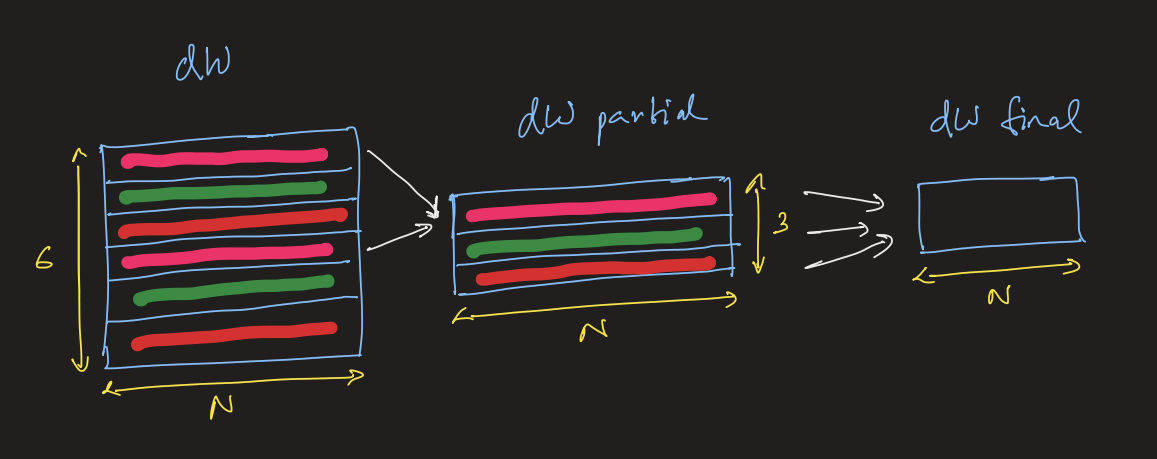
The reduction from dW to dW_partial is simple where we assign one program to each row but for reducing dW_partial to dW_final we do it in groups of BLOCK_SIZE_M. This is mainly due to the fact that unlike stage 1 (dw -> dw_partial) which was somewhat compute intensive with the calculation of dX as well in this stage we are purely doing reduction.
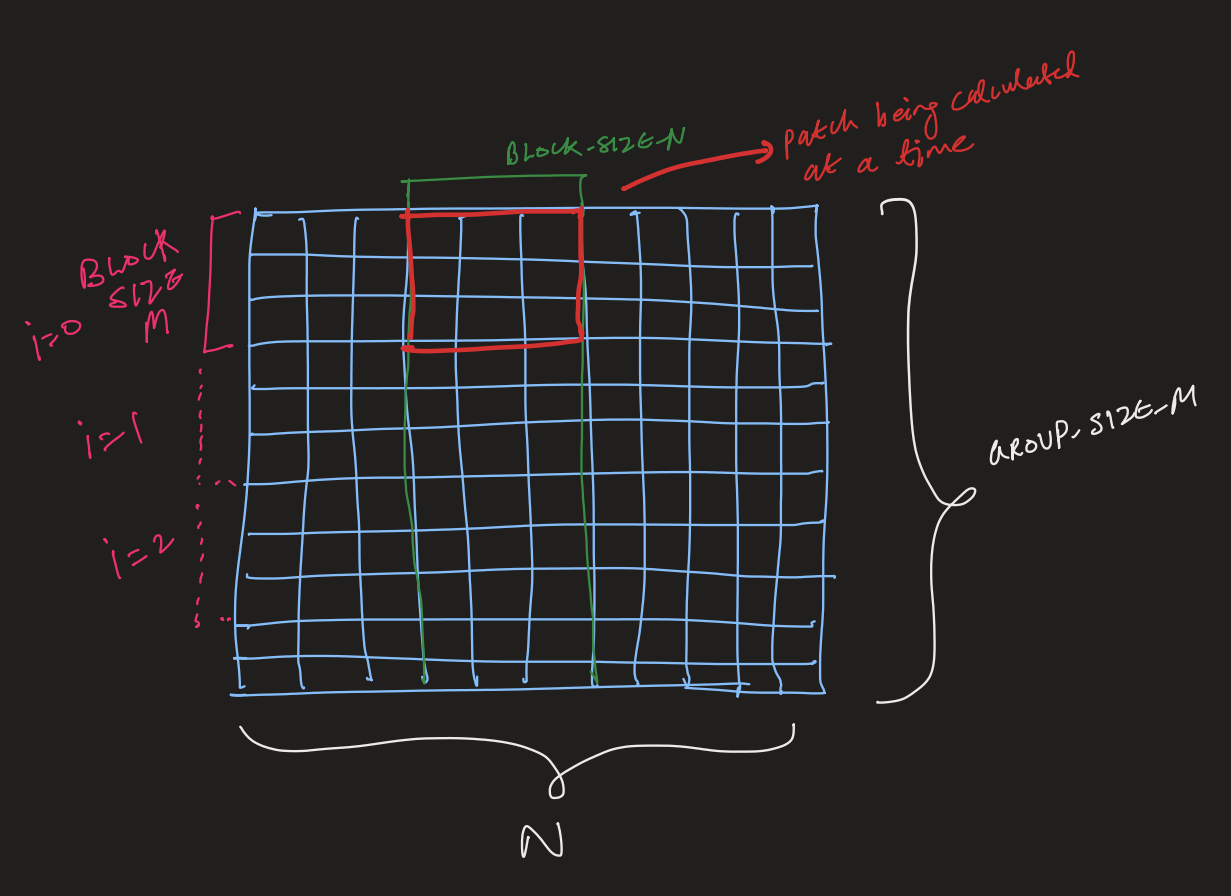
BLOCK_SIZE_N is basically N in the tutorial code but it can be better found through auto-tuning. To adapt this code for diffusion transformers last three dimensions should be taken into consideration for normalization (B, C, H, W) -> (B, C * H * W).